I have been coding at least since 2013. I started off self taught and now I’m majoring in CS, while still constantly learning outside of classes. I went from language to language, but something that almost always followed me was the idea of a prime number generator.
I must’ve tried this in almost every language I’ve used. It’s a very simple idea: create a console based program that can both check if an integer is prime, and print out a list of primes in order as quickly as possible. Usually, I don’t get too far for reasons I’ll get into. Although, I did succeed mostly with C++. I had an incredibly quick program (once I realized how terribly slow it was to print out the results to the screen) that ran on multiple threads and could fill up a file with prime numbers. I had two main problems: the file it filled up became so big that notepad wouldn’t be able to open it and the max size of an unsigned long.
Looking back at that code, it was a horrible mess and I’ve come a long way in both C++ and general code design. However, ever since then my quest began to create a data structure from scratch that could allow me to handle enormous primes. I managed to create a class that used strings to hold values. I defined all necessary arithmetic operations and it worked. Incredibly slowly. I should also mention that while I’m constantly coming back to this idea, my attention wanes as I run out of time between vacations.
Using strings was a horrible idea. Not only are they really slow when you try to treat them like numbers, but they are a huge waste of memory. Each character is 1 byte and in base 10 I would only be using 10 values per character. Even using base Z (where I use 0-9 and then a-z and finally A-Z), it would be a very stupid waste of space. So I started thinking about how I could store numbers more efficiently. In C++, it really isn’t that hard.
The solution I came up with involved std::size_t’s (size_t). It’s just a compiler name for the largest possible unsigned integer. Since I have a decent background in number bases (see my blog post on Duodecimal and why we should all switch to it), I was inspired. My design was a linked list structure of size_t’s. I used a linked list rather than an array because I wanted “small” numbers to not take up a lot of space, I wanted to avoid reallocation, and I also wanted to prevent an upper limit for the size. In theory, this object can be as large as memory allows. If I used something like a std::vector, it’s size itself is stored as a size_t.
Each size_t is the largest possible integer in C++. And each node in the linked list acts like a digit of a base. Let n be the largest size_t number. Suppose you have n + 1. That number would basically just be 1<—>0 in this form. Then you keep ticking up the 1’s digit, etc. This means that the numbers are stored incredibly densely. We’re dealing with base (n+1). In my case, I think n is 64 bits. So n=264 – 1. Anyway, to store n2 , you would need 2 nodes. To store nk you only need 64*k bits.
This is insanely better than using strings. Since they’re integers already as well, I get to avoid conversion. My problem recently has been finding the time and motivation to work on this. I try to create unit tests so I can guarantee it’s working as expected and I get bored. I also need to find efficient algorithms for arithmetic operations.
Despite my inability to complete this project, it does a good job of showing the benefits of Object Oriented Programming. I can take all of this complexity and shove it into a class. Once that class is done, I can create the functions to simply calculate primes the normal way.
Checking Primality
The most basic way to check if an integer is prime is to check if any positive integers less than it (other than 1) divide it. From there, you might realize that you can skip all of the even numbers after 2 because if 2 doesn’t divide it, then neither will any of the evens. Then you can also skip all integers larger than it’s square root as factors come in pairs. A few proofs would easily show these results to be true. Then you can continue to progress downwards. However, I’ve come up with a method as well.
How come after you check 2 you can skip all of the even numbers? Okay I suppose I should do one simple proof here:
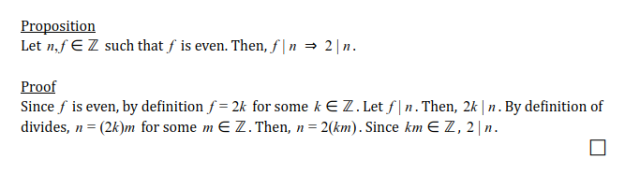
In fact, let me do this in general:
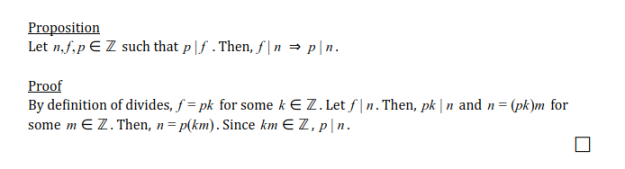
I enjoy a nice simple proof every now and then, even though I could’ve just cited transitivity of divides. Anyway, what this is telling us is that this applies for any factors. Any time an integer does not divide our potential prime, we can ignore all multiples.
What I’m getting at is that the hypothetically most efficient method for verifying primality is to check all primes up to it’s square root. Since every number is either prime or the multiple of primes, checking a prime also checks every single multiple of that prime. The problem is that you need a list of primes to check. Hence, my program would store primes and use them to verify if a number is a prime.
You may be thinking that if I have a list of primes, why bother at all with arithmetic. And thinking about it, having an “exhaustive” list of primes (an exhaustive infinite list…) and simply checking that list could be very efficient to verify a number is prime. However it would be pretty inefficient to verify that the average number is not prime. The reason I’m not using that method is because my list of primes is small and slowly grows. I only need to store primes up to the square root recall. That means to check 100, I’ll only have 2,3,5, and 7 stored. To check 10,000, I’ll only have all 2 digit primes.
So as I verify primes the list would grow and add more factors in order. You would also want to check the smaller primes first. While you can’t exactly say that more integers are even than are multiples of 5 due to the set being infinite, any complete finite subset of consecutive integers has this property. Multiples of 2 will make up half of the elements, multiples of 3 one third, etc. So you’ll want to start with the smaller primes first.
How to determine divisibility is also up to you. For instance, in base 10 we can rule out any integer who’s first digit is a 0 or 5 (except the number 5 itself) since that rules out multiples of 5 and 10. However, when working with duodecimal, I realized different number bases have different properties for divisibility. For example, in base 12 every multiple of 4 and 8 ends in 0,4, or 8. Every multiple of 3 and 9 ends in 0,3,6, or 9. Every multiple of 6 ends in 0 or 6. Every multiple of 12 ends in 0.
You could potentially have an algorithm to convert the integer to a different number base that is more efficient than performing an arithmetic calculation. Especially considering that for these tricks, you only need to convert the first few digits of the number. I think it’s a really interesting idea, however you risk circumventing the benefits of the machine code. Often times you try to make something more efficient, and then it’s either unnecessary or makes performance worse because the compiler was able to do a better job “fixing” your code. I think either way I’ll have to experiment with these idea in the future. Thinking about it, you only need to convert the number to the base of the prime and then check if the 1s digit is 0. You can then modify how many digits you actually convert based on how many digits the base-prime number will be. For larger numbers this might have potential.
Conclusion
While this project may not be the best example, I think it’s very useful for programmers to have a “go to” project for practicing an unfamiliar language. Something simple enough to allow you to write it from memory, while complex enough to give you a good grasp of the language. In this primes project, I have to handle the terminal, arithmetic, functions, objects, files, threads, etc. If I simplified it down and ignored my ambitions, it would server as a very functional example to allow you to learn the syntax and libraries of a new language. Ideally, you wouldn’t even have the original code to look at. You would just program the functionality from memory using your IDE and Google to figure out syntax. The best way to learn a language is to use it. If you have something familiar in your mind, then you have a great example project to work on already. I find struggling to implement functionality and spending a lot of time searching for a solution has taught me an invaluable amount about the languages I use.
From the blog CS@Worcester – The Introspective Thinker by David MacDonald and used with permission of the author. All other rights reserved by the author.
